where λ (lambda) is wavelength, ν (nu) is frequency, and c is the speed of light

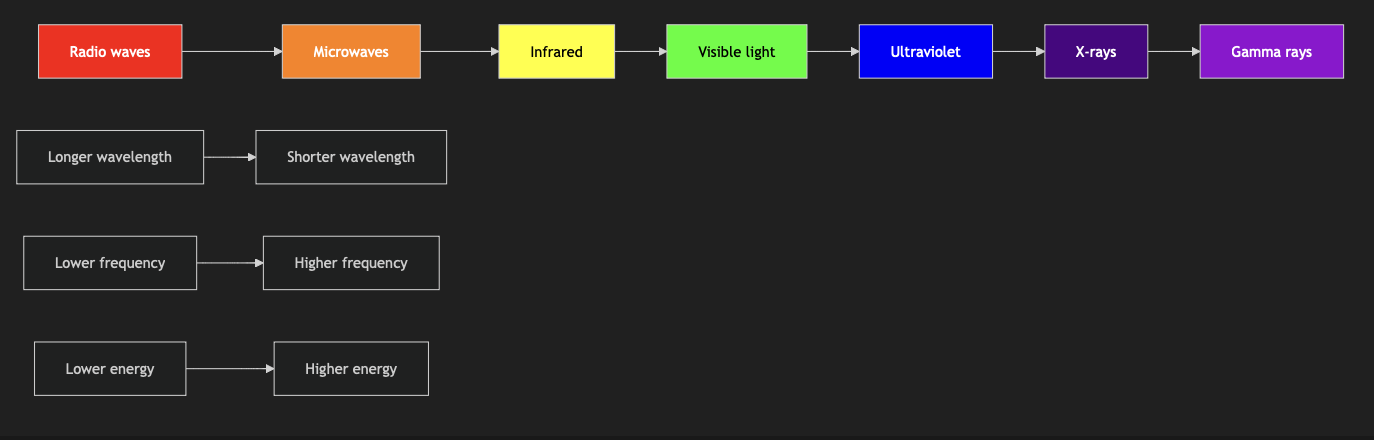
This graph represents the electromagnetic spectrum, showing the progression from radio waves (longest wavelength, lowest frequency, and lowest energy) to gamma rays (shortest wavelength, highest frequency, and highest energy). The colors approximate the visible light spectrum.

quantum (meaning “fixed amount”) is the smallest quantity of energy that can be emitted or absorbed as electromagnetic radiation.

the energy E, of a single quantum equals a constant(h) times the frequency(v) of the radiation:

h ⇒ Planck constant

Einstein proposed that radiant energy striking a metal surface behaves like a stream of tiny energy packets. Each packet, akin to a "particle" of energy, is called a photon. Building on Planck's quantum theory, Einstein deduced that each photon's energy is equal to the Planck constant multiplied by the light's frequency.

A spectrum is produced when radiation from such sources is separated into its component wavelengths

The integer n, which can have whole-number values from 1 to infinity, is called the principal quantum number.

The lowest-energy state (n = 1) is called the ground state of the atom. This state is analogous to the bottom rung of a ladder. When the electron is in a higher-energy state (n = 2 or higher), the atom is said to be in an excited state.

De Broglie suggested that an electron moving about the nucleus of an atom be-
haves like a wave and therefore has a wavelength. He proposed that the wavelength of
the electron, or of any other particle
, depends on its mass, m, and on its velocity, v:

The quantity mv for any object is called its momentum.
De Broglie used the term
matter waves to describe the wave characteristics of
­ material particles.

The second quantum number—the angular momentum quantum number, l—can have integral values from 0 to n - 1 for each value of n. This quantum number defines the shape of the orbital. The value of l for a particular orbital is generally designated by the letters s, p, d, and f, corresponding to l values of 0, 1, 2, and 3:

Value of l: 0, 1, 2, 3
Letter used: s, p, d, f

The magnetic quantum number, ml, can have integral values between -l and +l, including zero. This quantum number describes the orientation of the orbital in space. ⇒ -1/2 or + 1/2

The collection of orbitals with the same value of n is called an electron shell. All
the orbitals that have n = 3, for example, are said to be in the third shell. The set of
­ orbitals that have the same n and l values is called a
subshell.

Orbitals with the same energy are said to be degenerate.

Energy = n + l

if energies are equal bigger n has more energy.